Rick's b.log - 2023/01/14
You are 3.147.6.176, pleased to meet you!
|
Rick's b.log - 2023/01/14 |
| It is the 21st of November 2024 You are 3.147.6.176, pleased to meet you! |
|
mailto: blog -at- heyrick -dot- eu
However, a combination of dyscalculia (that's messing up numbers) and a lack of time to get around to thinking about it meant that decades passed by and nothing got done.
Until today.
I suppose one of the main hindances, sadly, was a series of articles back in the Spring and Summer of 1997 in Acorn User called "Virtuality" that repeated endlessly that the whole thing was "complicated" and that one should contact the author if more explanations were required.
Unfortunately, all of that was complete bollocks. It is actually surprisingly simple. The core code for a very simple raycaster can fit into a screenful or two.
So what I am going to present you with today is what the Acorn User article should have started with - a simple BASIC program that will perform the rendering. It may take somewhere between eight and thirty centiseconds to draw a screen (meaning something between 3fps and maybe 12fps, purely for the drawing).
Slow, yes. Too slow for making a game with. But on the other hand you'll get to understand how it actually works. Once you understand what's going on, then (and only then) should redraw speed and optimisations become a concern.
What follows is pure simple BBC BASIC. Not a single line of assembler in sight. It'll work on anything from a RiscPC onwards.
This code and the method is based upon that presented by Lode Vandevenne. The reason for choosing this is because it works rather differently to most other raycasters in directly using vectors instead of maintaining the direction as an angle and converting. For some reason, this has led to a method and corresponding source that is delightfully succinct. It does suffer in that it requires a competent floating point unit, so you might not want to write this in C just yet if you have the DDE.
To ram home the point, here is a screenshot of a squished version of the entire program. Okay, fair enough, I've used a small font size. But it's still readable and it... is actually really compact.
But before I look at what ray casting is, we must first look at ray tracing.
More advanced science will tell you that there's no such thing as a 'ray', it's a never-ending stream of photons. It also will have explained that we see in colour because (whitish) daylight contains all sorts of different colours all mixed together. We see grass as green because the blue, red, yellow, etc are all absorbed, and green is reflected. So it's the green that we see. And so on.
Ray tracing is the manner of faking this in a computer. Since trying to calculate what comes from all of the possible light sources in the virtual world into the virtual eyeball would take until the heat death of the universe, it instead performs the calculation backwards.
Clearly, for a simple game such as the likes of Wolfenstein, waiting for frames to render would not be a particularly immersive experience. You see a Nazi soldier, you mash the fire button, then you go make a cup of tea while the computer churns through the animation of that happening. Uh, no, just no.
What ray casting does is epic cheating.
As you know, a screen is made up of pixels in two dimensions. There's horizontal, across the screen, and there's the vertical up and down. The beginning of The Twilight Zone would have made that part quite clear. ☺
Instead of attempting to work out the value of every single pixel on the screen, what ray casting does is to split the screen into a set of vertical strips. That is to say, columns going from left to right across the screen.
If I blank out every other column, you can see what I mean...
For each screen column, two rays are "cast out". That's a weird expression, because to me being cast out is like "away with you, and never darken my doorstep again", but I'm not the one who named it. Anyway, two rays are cast out for every column across the screen.
These rays travel together (I'll explain why two shortly) and they move out from the viewer's position until something is hit.
When something is hit, this gives us a reference in our "map", which tells us three things. What was hit, what side of it, and how far away it is.
Knowing what was hit allows us to know what colour (or texture) we should use to draw the object. And knowing how far away it is allows us to know how big to draw it.
Let me repeat that.
That we end up with something that looks sort of 3D on the screen is great, but that illusion is the only part of this entire process that is in any way three dimensional.
We have a map, of so many elements across, and so many up and down. This map will be filled with numbers. A zero represents nothing, an empty square. Non-zero means there's a wall block there. The number can relate to colour, texture, or what-have-you.
We use floating point (that is, numbers with fractional parts) because the viewer position and the rays do not jump from one element to the next. There's a lot more finesse than that. So the viewer position may well be "four and two fifths". That's perfectly fine.
But when we are working our way around the map, we are going left and right and/or up and down in the array. This will make a little more sense once you've seen the map (it's just below), but keep in mind at all times that everything that happens is two dimensional.
That means the map looks like this, with the viewer's location in blue.
However, the initial viewer position is on the right, looking left. So while the map is as shown, it might help to flip it so we can better see how it relates to that which is actually drawn on the screen.
It's still hard to work out, isn't it? So let's try again. This time we'll draw a little grid, colour the squares as appropriate, and add some lame "perspective" to help. Try this:
Ah, now we're getting somewhere.
We start at the viewer position (marked V), and cast out rays sweeping across the screen. For each ray cast, we will be stepping through the map (away from the viewer position) until we reach a square that contains something.
The normal way to calculate the hypotenuse is to know that the square of the hypotenuse is the sum of the squares of the other two sizes. One side is 1, the size of a map square. The other side one plus the square of the Y ray divided by the square of the X ray, which indicates how far the X ray must travel in the Y direction in order to make an X step. I'm not entirely sure how this works, it just does so I'm not going to argue.
But how far is the X step? That's the delta. It is derived from
This diagram, actually, was the breakthrough that I needed to understand how raycasting works. I knew the basic principle (it's not hard), but not how it was actually done. I'm still not entirely sure how the SRQ calculation works, but seeing how it was used to derive the hypotenuse and thus the step value, it makes a lot more sense now.
Now that we know the size of the triangle (and thus our delta), we can simply fudge this with our current offset within a map square to determine a location representing how far the ray has to travel for each step of a square. In this case, as it's the X ray, it has to go up 1.85 squares in order to go left one square. It doesn't have to precisely hit the edge of the correct square, it just has to be within the square and in correct ratio with the Y ray in order that we can tell which one hit first should they both result in a hit.
You'll notice I'm talking about X rays and Y rays. This is correct. You see, if we sent out just one ray, we would be endlessly calculating the size of the next step from our current ray position. This would be a lot of, mostly unnecessary, work.
We keep track of the horizontal boundaries and the vertical boundaries separately. After we check a ray, the next step point is added to it. This works because our rays always move in a straight line, together. So adding the appropriate delta to either the corresponding ray will simply step to the next boundary that needs to be checked.
But we are looking at a screen. A little rectangle into a virtual world. Because of this, our field of view is reduced. For a VGA/SVGA screen, a field of view of 66° is good.
As you can see, 66° is the only one where the green square directly in front of us looks square.
Why this is important is because it determines how we sweep across the screen. In which direction does the leftmost ray go? The rightmost one? And how much is there between each screen column?
What we can see from this is that removing comments can speed up a program, but changing SWI names to numbers makes little difference in reality (it calls ColourTrans to set the colour for each strip).
However, as I said above, it's this version of the code tested on this machine (which due to looping and such isn't identical to the code given here). It's not an absolute, just a comparison of one method against another.
Anyway, enough exposition, let's start looking at some source.
This sets up an error handler, picks a 256 colour VGA mode (MODE 28), and defines the screen dimensions.
Now the map is defined. As indicated, there are four square types - red, green, blue, and empty.
This sets up the initial map location (14,4), and also defines the direction and projection plane values. These are perpendicular to each other.
Here is an example of how to perform a rotation to whatever angle. PI means to rotate 180°, as radians are PI×2 for a complete circle.
Note that if you get values like
BASIC only starts doing this at E-3, which means the value is
That's it for the setup.
No, seriously, that's it.
There are no complicated sine/cosine tables to build.
The
You could also use
To give an idea of what I mean by the ECF dithering, here's an example with the colours fiddled to show the effect. Zoom in, you'll see what I mean.
As the comment says, we do the simple stuff first.
Now for the not-so-simple stuff. ☺
angle performs a sweep across the screen with -1 being the left, 0 being the centre, and 1 being the right.
The only thing that needs explaning here is why we're setting the delta to be 12,345,678. It's a dummy value that is far too large to be encountered normally, but non-zero so there's no risk of causing an FP exception (like divide by zero). It's basically setting that ray so far away that we'll be stepping the other one repeatedly until something is hit.
Now we perform the appropriate calculation for each ray depending upon whether it's positive (up/right) or negative (down/left).
We now know our step values and directions (a map square at a time) as well as our initial starting point (the first boundary), to which the delta (distance to the next boundary) is added.
Now it's time to actually cast the ray.
Yup. That's it. If nothing has been hit (the map square is a zero), then we simply increment whichever ray is the shortest one, and check again. If we're going at, say, a 45 degree angle then the two rays will leapfrog each other until something is hit. If it's a steeper angle, then one ray may be bumped a lot while the other doesn't move as often. You can visualise this yourself with a piece of squared paper.
Since the closest ray is the one that hit, we can also use this to tell which side (top/bottom or left/right) was hit. This allows us to add some subtle shading to make things stand out better.
Now we need to correct the ray's 'hit' location to determine the actual wall distance.
The offset at the end is so we don't have a projection 'through' the wall if we're close to it. That would be bad. Kittens would suffer.
So now we know our three important things. We know what sort of wall was hit (from the map), we know what side was hit, and we know how far away it is (thus how big to size it).
The horizontal centre of the screen is the point where the floor and ceiling meet. The walls are centred on this point, growing in size (both up and down) as they are closer. This creates the illusion of distance.
There's only one more thing that we need, and that's to work out the appropriate colours.
Horizontal boundaries are drawn in half-brightness colour, and if it's a vertical boundary, it's full brightness. It's visually unrealistic, but helps the illusion of three dimensions by making the different sides stand out. Verticals are full brightness because we begin facing left, so it's what we'll see head on.
Finally, plot this sliver of wall to the screen, and loop around for the next one.
The ScreenSave at the end drops a copy of the rendered scene to your storage, as "_3dsceneHHMMSS" in the root directory of the current filing system, where HHMMSS is the current time, unless you hold down the Alt key.
Writing this has taken a long time. Weeks of reading through all sorts of sources, performing endless calculations with my calculator (and getting most wrong until pennies were dropped). Then the diagrams and graphics and such.
However I very much hope I've done a reasonable job of showing how raycasting works. There are other methods, but the underlying principle is the same.
Now, all you're missing is the source (Zip, 4173 bytes).
Have fun!
Basic ray casting
For many years I have wanted to understand how ray casting works. That is to say, the sort of world building as used in games such as Wolfenstein, Doom, and so on.
The code provided was, itself, quite hairy, rapidly delving into optimised assembler to get a decent redraw speed on the 8MHz machines typical of the time. This had the effect of making it quite incomprehensible. Because it was "complicated".
What would take much more explanation is the how of it. The code is short and simple but the maths is mind melting.
The reason it won't work on earlier machines is because I use the R,G,B form of GCOL instead of mucking around with colour and tint values. If you fiddle the GCOL lines accordingly, it ought to work on any RISC OS 3 machine (I don't think RISC OS 2 had MODE 28?).
However, BBC BASIC compiled with ABC in VFP mode is pretty damn fast. As is regular BASIC. Some comparisons below.
Anyway, while trying to get my head around the maths, it just seemed to me that Lode's method had the fewest hoops to have to jump through. Other raytrace sources may be faster, using integer maths and lookup tables, but it seemed to me that all of these things obfuscated what was actually happening. The basic method is the same, the difference is how one gets there.
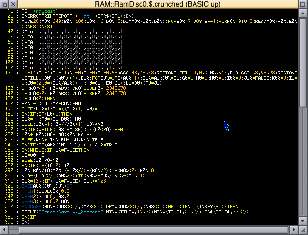
The entire program - yes, this is it, all of it.What is ray casting?
Ray casting is the ability to draw a world that looks three dimensional. For the purposes of this demonstration, we shall be drawing this:
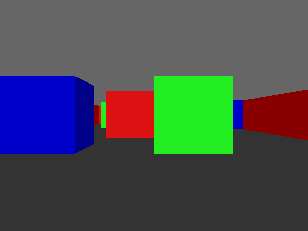
Our colourful world.So, what is ray tracing?
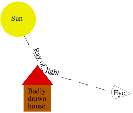In science class you should (!) have learned a little about how we see things. Rays of light come from a light source, such as a bulb or the sun, and bounce off of objects. These rays of light then enter our eyes where we perceive them, as demonstrated by the naff drawing on the right.
For every single pixel on the screen (a dot of the final image), it will calculate a 'ray' coming back out of that single pixel, and it will step through the data that makes the virtual world until that ray hits something. Then, according to the texture of what it hits, that ray might be reflected until it hits something else (ray tracing newbies really like creating reflective spheres). Eventually, that ray will meet an end point. And that end point determines how the pixel will be set. More or less. You can do clever things like distance distortion or fogging, but you get the idea. One pixel done, move to the next one, repeat.
The end result is a virtual world such as is seen in a lot of 3D-style animations these days.
So, then, what's ray casting?
In order to create a full 3D-style animation, it takes powerful computers a lot of time. Older productions such as the movie Toy Story were generated using render farms. That is a whole pile of computers (117, in that case) churning out the frames that make up the movie, one by one. Depending on the complexity of the frames, the fastest were done in about 45 minutes. The more complex took over a day. Per frame. Of course, this was done back in 1998-1999 when computers were a fair bit slower.
Ironically, the render time of the latest Toy Story film was about the same. The more modern computers are a lot more capable, but this didn't translate into quicker render times, it translated into more complex imagery.
Drawing the world in vertical slices.
Once we have those pieces of information, we simply draw a line either side of an imaginary centre point (you'll notice in the picture above that the middle of the screen (vertically) is the exact middle of everything) and hey presto, a bit of wall has been drawn. Onto the next strip, churning through the columns until the end of the screen has been reached.
Wait, you said there are two rays?
Yes. But to understand why, we first need to look at what's actually going on. So, let's backtrack a little.
FIRST, KNOW THIS
We are working strictly in two dimensions.
WE ARE WORKING IN TWO DIMENSIONS.
The sole and only three dimensional part is what we fake up on the screen.
The map
The map is a simple array. In our example, it is built up as follows:
REM The size of the 2D map
REM Let's keep it simple for now
mapx% = 16
mapy% = 8
DIM map%(mapx%, mapy%)
FOR loopy% = 7 TO 0 STEP -1
FOR loopx% = 0 TO 15
READ map%(loopx%, loopy%)
NEXT
NEXT
REM 0 = Empty
REM 1 = Red square
REM 2 = Green square
REM 3 = Blue square
DATA 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1
DATA 1,0,0,0,3,3,0,0,0,0,0,0,0,0,0,1
DATA 1,0,2,0,0,0,0,0,0,0,0,0,0,0,0,1
DATA 1,0,0,0,3,0,0,0,1,0,2,0,0,0,0,1
DATA 1,0,3,0,0,0,3,0,1,0,0,0,0,0,0,1
DATA 1,0,0,0,2,0,0,0,0,0,3,0,0,0,0,1
DATA 1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1
DATA 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1
REM /|\
REM |
REM Viewer is here, fourth row up. looking to the LEFT.
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 0 0 0 3 3 0 0 0 0 0 0 0 0 0 1
1 0 2 0 0 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 3 0 0 0 1 0 2 0 0 0 0 1
V
1 0 3 0 0 0 3 0 1 0 0 0 0 0 0 1
1 0 0 0 2 0 0 0 0 0 3 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 11 1 1 1 1 1 1 1
1 0 0 0 0 0 0 1
1 0 0 3 0 2 0 1
1 0 0 0 0 0 0 1
1 0 2 0 3 0 3 1
1 0 0 0 0 0 3 1
1 0 0 3 0 0 0 1
1 0 0 0 0 0 0 1
1 0 0 1 1 0 0 1
1 0 0 0 0 0 0 1
1 0 3 0 2 0 0 1
1 0 0 0 0 0 0 1
1 0 0 0 0 0 0 1
1 0 0 0 0 0 0 1
1 0 0 0 V0 0 0 1
1 1 1 1 1 1 1 1
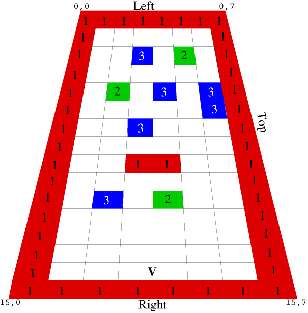
Visualisation of the map.Why two rays, then?
The reason we use two rays is because it is time consuming and pointless to step away from the viewer position in little hops, and if we used big hops there is the risk of missing corners.
Instead, we can work out four constants. The first two are the distances between the viewer position and the next vertical boundary, and the distance between the viewer position and the next horizontal boundary.
The second two are the "deltas", the distance from one boundary to the next. Pythagorean maths.
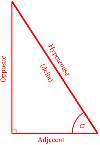What we actually do here is to solve the triangle first. We know one side of the triangle will be '1', as it traverses one square. The angle is simply the current angle we're actually facing. For example, X = -0.54. It is a negative value because it's to the left. Left and down are negative, up and right are positive.
The angle is then translated into an X and Y ray by transforming them with the projection plane. This is a little complicated, but boils down to the X ray being the X direction plus the X projection multiplied by the screen offset angle.
In our test, the X ray is -0.54, whilst the screen offset is 0 (middle of the screen), and the X projection doesn't matter as anything multiplied by zero is still zero.
The corresponding Y ray is 0.84. Don't worry right now about how this value was obtained (if you must know, I used the rotation code given below).
SQR(1 + (Y * Y) / (X * X))ABS(SQR((X * X) + (Y * Y)) / X)
This 'simplification' is important, because it means we can cheat massively and simply set the X delta to ABS(1 / X)
In each case, it results in a value of 1.85 which is the length of our X delta for the angle -0.54 (which is about 31° to the left, or a direction of about 329°).
Instead, we can manage two rays that travel in tandem. One is sized to the next horizontal intersection of the map, and another ray that is sized to the next vertical intersection of the map.
Then we simply look at whichever of the two rays has the smallest value (is closest). If there's nothing there, we add a step to that ray (not the other) and check again, only paying attention to the state of the closest ray each time.
Doing it like this means that when a wall is hit, we will know which ray actually hit the wall - it'll be the smallest (closest) one.
Field of view
In order to create a good looking result, we need to sweep from left to right, but with restraint. With a squarish screen, as VGA would offer, a good value is to have somewhere between 65-70° visible. This is our field of view.
Human eyes have a pretty impressive field of view. If you hold out a finger in front of you, then move your arm backwards without moving your eyes, you'll still be able to see your finger when your arm is almost held out to the side. Each eye offers around 135° of vision, and the two together gets closer to around 165°.
Here are some examples of different fields of view:
Obviously, if we were using a widescreen mode, we have a greater width and thus would require a wider field of view.
You can see this on the following diagram where I have indicated the first and last ray, along with an arrow to show our direction.
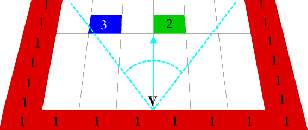
The leftmost and rightmost rays.Render speed
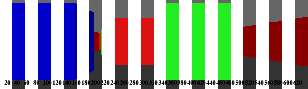
Just by way of example, on a Pi 3B+ (1400 MHz), drawing the screen 100× in MODE 28 results in the following speeds.
These should be taken with a pinch of salt as it's only the render, there's nothing else, and it relates to this machine. Other machines (Pi 1B, Titantium, RPCEmu, etc) will obviously be different. But it's an interesting exercise in variations.
Four source versions were created:
Additionally:
What Time 100× Time/frame FPS Original 492 cs 4.92 cs 20 fps Crunched - BASIC64 FPA 475 cs 4.75 cs 21 fps No comments, SWI names 380 cs 3.80 cs 26 fps No comments, SWI numbers 376 cs 3.76 cs 26 fps Crunched - normal BASIC 280 cs 2.80 cs 35 fps Crunched - BASIC64 VFP 259 cs 2.59 cs 38 fps Compiled FPA 240 cs 2.40 cs 41 fps Compiled VFP 143 cs 1.43 cs 69 fps
Crunching can nearly double the speed; especially since we're turning 8K of code into 1.3K of code!
The lower accuracy BASIC FP routines are almost as fast as using hardware FP, and since FPA emulation is so slow, a compiled version using FPA is only slightly faster than a plain crunched version in regular BASIC.
But compiled using hardware FP? It flies, blasting past the 60fps barrier and not quite making 70fps. Though in reality there would be plenty of extra code in a real program for dealing with player movements and such, so 50-60fps could be expected... though non-compiled BASIC doesn't have a hope of anything over 25-35fps, and original source with comments would be Far. Too. Slow. to even think about.
Now for some code!
This code makes much use of floating point. I trust the above chart indicates the RISC OS specific issue where we get screwed due to a continued reliance upon an emulated floating point maths processor...which is nuts when most (if not all) current ARM devices offer hardware floating point maths.
Getting started
REM >raycast1
REM
REM Rick's simple ray-caster, version 1
REM https://heyrick.eu/blog/index.php?diary=20230114
REM
REM Basic demonstration of principle
REM
REM The principle is as described by Lode Vandevenne at
REM https://lodev.org/cgtutor/raycasting.html
REM
REM What's worth noting here is that we do *NOT*
REM work in degrees like a normal ray-caster, so
REM the code that follows is rather more compact
REM than you may see in other places, but it does
REM require competent floating point maths support.
REM
ON ERROR PRINT REPORT$+" at "+STR$(ERL) : END
REM 640x480 in 256 colours; it's VGA so
REM everything ought to support this.
MODE 28
REM The physical size of the screen
width% = 640
height% = 480
REM The size of the 2D map
REM Let's keep it simple for now
mapx% = 16
mapy% = 8
DIM map%(mapx%, mapy%)
FOR loopy% = 7 TO 0 STEP -1
FOR loopx% = 0 TO 15
READ map%(loopx%, loopy%)
NEXT
NEXT
REM 0 = Empty
REM 1 = Red square
REM 2 = Green square
REM 3 = Blue square
DATA 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1
DATA 1,0,0,0,3,3,0,0,0,0,0,0,0,0,0,1
DATA 1,0,2,0,0,0,0,0,0,0,0,0,0,0,0,1
DATA 1,0,0,0,3,0,0,0,1,0,2,0,0,0,0,1
DATA 1,0,3,0,0,0,3,0,1,0,0,0,0,0,0,1
DATA 1,0,0,0,2,0,0,0,0,0,3,0,0,0,0,1
DATA 1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1
DATA 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1
REM /|\
REM |
REM Viewer is here, fourth row up. looking to the LEFT.
REM Note that as of now, it's lots of floating point maths
REM Where in the map does the viewer start?
ourx = 14
oury = 4
REM Looking to the left
xdir = -1
ydir = 0
REM The projection plane, in 2D
REM This is perpendicular to the direction.
xproj = 0
yproj = 0.65
REM yproj being 0.65 above corresponds to a field of view of
REM about 66 degrees, which is a good value for a old style
REM squarish screen, such as the VGA mode used here.
REM If using a 16:9 display, you'll need a wider field of view
REM because of the extra width. Try 0.85 which equals a field of
REM view of about 80 degrees.
REM
REM To convert the above value into degrees for a viewing angle:
REM value = 0.65
REM PRINT ((ATN(value / 1) * 2) / PI) * 180
REM (this converts the value into radians, and then into degrees)
REM
What this means... hold your thumb out at arm's length in front of you. You, and your left/right are the direction, and your thumb is the projection. To understand how the projection works, use both hands to make a square to look through, like cliché movie directors. As you move closer, you can see more, right?
The only difference is that in a ray caster, it creates distortion (as shown above, the fat and skinny squares) because the screen size remains the same, so you're trying to fit a different view into the same screen size. But it's a workable description of how altering the projection distance alters what appears on the screen.
Because it must be perpendicular, the projection has to change as the direction changes. If these two are out of alignment, you'll get weird effects like skewed rectangles.
You have a copy of the source. Feel free to mess with the values to see what happens.
Choosing which way to face
Looking xdir ydir xproj yproj Left -1000.75Right 1000.75Up 010.750Down 0-1-0.750REM Rotate 180 degrees
rot = PI
oldx = xdir
xdir = (xdir * COS(rot)) - (ydir * SIN(rot))
ydir = (oldx * SIN(rot)) + (ydir * COS(rot))
oldx = xproj
xproj = (xproj * COS(rot)) - (yproj * SIN(rot))
yproj = (oldx * SIN(rot)) + (yproj * COS(rot))
-6.076E-11, this is the scientific notation for that number with ten zeros before it, in other words it's the same as -0.00000000006076.
Which means, just set it to zero.
0.00xx, so I think that any value that has an E- notation is probably safe to be ignored and set to zero.
This is done when we're working in degrees (and/or with integers) because it's mathematically expensive to keep switching from degrees to radians and calculating this stuff, so lookup tables are quicker. Since we work directly in radians (sort of), we lose the ability to easily say "we're facing northwest", but we gain in not having to keep converting from degrees.
Drawing the background
We shall simply set a dark grey floor and lighter grey ceiling.
REM Draw the floor
GCOL 48, 48, 48 : REM Dark grey
RECTANGLE FILL 0, 0, (width% << 1), height%
REM And now the ceiling
GCOL 98, 98, 98 : REM Lighter grey
RECTANGLE FILL 0, height%, (width% << 1), height%
<< 1 translates pixels into OS units for drawing on the screen. As MODE 28 is a 2:2 mode, one pixel is two OS units (in each direction). So we simply plot a rectangle of half the screen's height at the bottom, and then we draw another shifted up to fill the gap. This is the ceiling.
SYS "ColourTrans_SetGCOL", &30303000,,,0,0 for the floor and the same with colour value &62626200 for the ceiling if you prefer. GCOL with an RGB triplet calls the same SWI, the only difference is that GCOL also sets the dither flag.
That's why the values chosen may seem a little odd. They were chosen to look good but not invoke the ECF dithering (which didn't look so good).
Personally, I prefer calling ColourTrans directly as I can control the ECF dithering, but for this example I'm going to use straight BASIC.
It's pretty cool that RISC OS can do this for itself, however the effect doesn't lend itself to large patches of colour (as appears here) because at the usual distances people are to their screens, it can be rather noticable.
Obvious dithering is obvious.Casting rays
This is where all the magic happens.
REM Now, cast rays for each scrcol across the screen, starting from the left.
FOR scrcol% = 0 TO (width% - 1)
REM Let's do the easy inits first.
REM For now, let's look to see what map location we are in.
mapx% = ourx
mapy% = oury
REM We use an integer here in order to lose the fractional part,
REM as in this case we don't care how far along in any position
REM the viewer is, only which block matches where the viewer is.
REM These two values represent the distance from our current
REM (exact) location to the next square boundary. This is
REM updated as we step along.
xedge = 0
yedge = 0
REM The step values are -1 if it's a negative step, or 1 if it's a
REM positive step. Initially zero as the stepping hasn't been set up.
xstep% = 0
ystep% = 0
REM Has a wall been hit?
wallhit% = FALSE
REM Which side was hit? FALSE for an X side, TRUE for a Y side
side% = 0
REM This will be the distance to the actual wall that we're going
REM to draw on the screen.
towall = 0
REM Now for the freaky maths
REM Calculate our angle offset for the desired screen column.
REM This goes from -1 on the left, to 0 in the middle, to 1 on the right.
angle = (2.0 * (scrcol% / width%)) - 1
REM Now set up two rays. Remember when we are talking about X and Y
REM we are talking about the GRID that represents the array that our
REM map is in. It isn't X,Y on the screen, or in some 3D space, it
REM is the imaginary X,Y divisions between array elements.
REM Or, to put it more simply, imagine that you have written the
REM contents map% on a piece of squared paper like you used in maths
REM class. The horizontal lines are your X positions, and the vertical
REM lines are your Y positions.
xray = xdir + (xproj * angle)
yray = ydir + (yproj * angle)
REM Now we work out how far we must step from one square edge to
REM the next. Since the rays travel in a straight line, we only
REM need to calculate this once.
IF (xray <> 0) THEN xdelta = ABS(1 / xray) ELSE xdelta = 12345678
IF (yray <> 0) THEN ydelta = ABS(1 / yray) ELSE ydelta = 12345678
REM To explain the above a little better, the actual calculation
REM would be:
REM xdelta = SQR(1 + (yray * yray) / (xray * xray))
REM but because we already did some of this calculation when sorting
REM out xray/Y above, and we're only interested in the RATIO
REM between the X and the Y, all of this can be simplified down to
REM simply dividing 1 by the ray distance.
Working out the ray direction is performed by multiplying the projection plane by the direction, and adding this to the (ray) direction (we're facing).
The reason we're adding the projection rather than just fudging it from the direction is because what is drawn on screen is not based upon the viewer's direction, it's based upon the location of the projection plane.
Why? Because what you're looking at is a projection (clue in the name!). Consider it like cutting a rectangle out of a piece of cardboard and then holding it at arm's length to look through.
It's also a useful way of getting around the freaky fisheye effect that can happen if you don't offset the projection from the viewer's absolute location (that's another expensive calculation that other raycasters may have to do).
When can this happen? Consider a ray that is directly vertical or directly horizontal. In this case, one ray will step, but the other simply won't move at all.
So setting it to a big value is a safe way to make it inactive.
REM Now we work out which stepping to use, and our initial distance
REM to the edge of the current square.
IF ( xray < 0 ) THEN
REM We're moving leftwards in the map
xstep% = -1
xdist = ( ourx - mapx% ) * xdelta
ELSE
REM We're moving rightwards in the map
xstep% = 1
xdist = ( (mapx% + 1) - ourx ) * xdelta
ENDIF
IF ( yray < 0 ) THEN
REM We're moving downwards in the map
ystep% = -1
ydist = ( oury - mapy% ) * ydelta
ELSE
REM We're moving upwards in the map
ystep% = 1
ydist = ( (mapy% + 1) - oury ) * ydelta
ENDIF
REM Now look for a wall
WHILE ( wallhit% = FALSE )
IF ( xdist < ydist ) THEN
REM The next X boundary is closer, so let's step to it
mapx% += xstep%
xdist += xdelta
side% = FALSE
ELSE
REM The next Y boundary is closer, so let's step to it
mapy% += ystep%
ydist += ydelta
side% = TRUE
ENDIF
REM Was something hit?
IF ( map%(mapx%, mapy%) <> 0 ) THEN wallhit% = TRUE
ENDWHILE
REM Do you see how the two rays worked here? They are both
REM being cast together at the same time, and we're simply
REM stepping to look at whichever happens to be the closest.
REM Now that we know that something has been hit, we can work
REM out the wall distance. This is easy, we simply subtract the
REM delta that we stepped over from the accumulated distance to
REM the next side.
IF side% = FALSE THEN
REM It's an X boundary
towall = xdist - xdelta
ELSE
REM It's a Y boundary
towall = ydist - ydelta
ENDIF
IF (towall = 0) THEN towall = 1
So let's work on sizing it.
REM Now we have the wall distance, work out how big this line should be
drawsize% = height% / towall
REM Now work out the lowest and highest pixel to actually draw on
REM the screen; clipping it if it goes off the screen.
drawbot% = (-drawsize% / 2) + (height% / 2)
IF ( drawbot% < 0 ) THEN drawbot% = 0
drawtop% = ( drawsize% / 2) + (height% / 2)
IF ( drawtop% >= height% ) THEN drawtop% = ( height% - 1)
Thus, the above calculates where we shall begin and end drawing our line for this column of the screen.
REM Now work out what colours we want
col% = 127
IF (side% = FALSE) THEN col% += 128
CASE map%(mapx%, mapy%) OF
WHEN 1 : GCOL col%, 0, 0 : REM Red
WHEN 2 : GCOL 0, col%, 0 : REM Green
WHEN 3 : GCOL 0, 0, col% : REM Blue
ENDCASE
REM And, finally, draw the line, with correction between
REM OS units and pixels for MODE 28.
MOVE (scrcol% << 1), (drawbot% << 1)
DRAW (scrcol% << 1), (drawtop% << 1)
NEXT
IF NOT(INKEY(-3)) THEN
OSCLI("ScreenSave $._3dscene"+MID$(TIME$,17,2)+MID$(TIME$,20,2)+MID$(TIME$,23,2))
ENDIF
Let's try that without the commentary
Here's the whole program again, without comments and without being split up. The whole program this time.
REM >raycast1
REM Rick's simple ray-caster, version 1
REM Basic demonstration of principle
ON ERROR PRINT REPORT$+" at "+STR$(ERL) : END
MODE 28
width% = 640
height% = 480
mapx% = 16
mapy% = 8
DIM map%(mapx%, mapy%)
FOR loopy% = 7 TO 0 STEP -1
FOR loopx% = 0 TO 15
READ map%(loopx%, loopy%)
NEXT
NEXT
REM 0 = Empty; 1 = Red; 2 = Green; 3 = Blue
DATA 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1
DATA 1,0,0,0,3,3,0,0,0,0,0,0,0,0,0,1
DATA 1,0,2,0,0,0,0,0,0,0,0,0,0,0,0,1
DATA 1,0,0,0,3,0,0,0,1,0,2,0,0,0,0,1
DATA 1,0,3,0,0,0,3,0,1,0,0,0,0,0,0,1
DATA 1,0,0,0,2,0,0,0,0,0,3,0,0,0,0,1
DATA 1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1
DATA 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1
ourx = 14
oury = 4
xdir = -1
ydir = 0
xproj = 0
yproj = 0.65
GCOL 48, 48, 48
RECTANGLE FILL 0, 0, (width% << 1), height%
GCOL 98, 98, 98
RECTANGLE FILL 0, height%, (width% << 1), height%
FOR scrcol% = 0 TO (width% - 1)
mapx% = ourx
mapy% = oury
xedge = 0
yedge = 0
xstep% = 0
ystep% = 0
wallhit% = FALSE
side% = 0
towall = 0
angle = (2.0 * (scrcol% / width%)) - 1
xray = xdir + (xproj * angle)
yray = ydir + (yproj * angle)
IF (xray <> 0) THEN xdelta = ABS(1 / xray) ELSE xdelta = 12345678
IF (yray <> 0) THEN ydelta = ABS(1 / yray) ELSE ydelta = 12345678
IF ( xray < 0 ) THEN
xstep% = -1
xdist = ( ourx - mapx% ) * xdelta
ELSE
xstep% = 1
xdist = ( (mapx% + 1) - ourx ) * xdelta
ENDIF
IF ( yray < 0 ) THEN
ystep% = -1
ydist = ( oury - mapy% ) * ydelta
ELSE
ystep% = 1
ydist = ( (mapy% + 1) - oury ) * ydelta
ENDIF
WHILE ( wallhit% = FALSE )
IF ( xdist < ydist ) THEN
mapx% += xstep%
xdist += xdelta
side% = FALSE
ELSE
mapy% += ystep%
ydist += ydelta
side% = TRUE
ENDIF
IF ( map%(mapx%, mapy%) <> 0 ) THEN wallhit% = TRUE
ENDWHILE
IF side% = FALSE THEN
towall = xdist - xdelta
ELSE
towall = ydist - ydelta
ENDIF
IF (towall = 0) THEN towall = 1
drawsize% = height% / towall
drawbot% = (-drawsize% / 2) + (height% / 2)
IF ( drawbot% < 0 ) THEN drawbot% = 0
drawtop% = ( drawsize% / 2) + (height% / 2)
IF ( drawtop% >= height% ) THEN drawtop% = ( height% - 1)
col% = 127
IF (side% = FALSE) THEN col% += 128
CASE map%(mapx%, mapy%) OF
WHEN 1 : GCOL col%, 0, 0
WHEN 2 : GCOL 0, col%, 0
WHEN 3 : GCOL 0, 0, col%
ENDCASE
MOVE (scrcol% << 1), (drawbot% << 1)
DRAW (scrcol% << 1), (drawtop% << 1)
NEXT
IF NOT(INKEY(-3)) THEN
OSCLI("ScreenSave $._3dscene"+MID$(TIME$,17,2)+MID$(TIME$,20,2)+MID$(TIME$,23,2))
ENDIF
END
And...?
There's loads more to cover. Wall textures, for example. Not to mention... movement!
So for now, I'm going to end it here and leave all the other stuff for another time.
You translate a direction into a pair of distances representing the next X boundary and the next Y boundary, then you step the smallest each time until something is hit. A bit of maths can turn the value into an absolute distance which directly determines how big to draw the wall piece.
There, a one-sentence summary.
Anon, 15th January 2023, 18:38
(You don't know how long I've been waiting for an opportunity to use that.)
I'd be interested to see how quickly that ran on an A5000 with FPA10 chip and a ColourCard Gold. I know that POVray on that hardware could ray trace faster than a StrongARM RiscPC.Anon, 15th January 2023, 18:41
https://www.imdb.com/title/tt0114709/
J.G.Harston, 15th January 2023, 18:54
Checks... ah, no, it uses 32-bit-specific arithmetic like a+=b, etc.
J.G.Harston, 15th January 2023, 19:13
Running on a Beeb is sufficiently slow that you can see what it's doing and so understand the process.Rick, 15th January 2023, 20:35 Anon, 16th January 2023, 21:16
Would be interesting to get some benchmarks for this.Rick, 16th January 2023, 21:31
On modern machines, it supports FPA and VFP, picking the appropriate one (though you can force it with *BASICFPA and *BASICVFP).
I've already made comparative tests on the 3B+, see above.J.G.Harston, 19th January 2023, 02:32
Anyway: https://www.youtube.com/watch?v=2YfqdcVB0kURick, 19th January 2023, 19:42
Did you do anything else to the code? Single letter variables and the like?J.G.Harston, 20th January 2023, 04:32
RECTANGLE to MOVE/PLOT 101
GCOL r,g,b to GCOL 0,RGB
Condensed multi-line IFs
Replaced a += b to a=a+b etcVinceH, 20th January 2023, 17:49
I've just taken delivery of an Acorn Electron, and I'd try it on that if I could - but unfortunately the seller didn't have a power supply for it, so I've no idea if it even works!J.G.Harston, 21st January 2023, 00:50
| © 2023 Rick Murray |
This web page is licenced for your personal, private, non-commercial use only. No automated processing by advertising systems is permitted. RIPA notice: No consent is given for interception of page transmission. |
